在廣告系統中，CTR， CvR等模型想必大家都非常熟悉了。將一個包含一系列特征值的樣本輸入CTR, CvR模型，模型輸出一個點擊率或者轉化率的預估值。有時候我們也會遇到一些情況，除了需要預估值之外，還需要知道預估值的不確定度（Uncertainty）（或者預估值的分布，有了分布，通常不確定度也能算出來）。
我們從三個問題引出今天的討論。
問題一: 什么是不確定度？
有些朋友可能對不確定度沒有什么概念。舉個例子：
廣告A: 3個展現1個點擊，因此點擊率為1/3
廣告B: 300個展現100個點擊，因此點擊率為1/3
這個時候我們對廣告A與B的點擊率預估值可能都是1/3，但是因為廣告A的樣本數很少，如果因為一些隨機因素少來一個點擊或者多來一個點擊，點擊率都會發生巨大變化，因此廣告A點擊率為1/3的不確定度要大于廣告B。從通俗的語言來理解，“不確定度”就是“預估準不準”的意思。如果點擊率模型會說話，它會說：“主人，我會把這兩個廣告的點擊率都預估為1/3，但是我對廣告A的預估沒什么把握，可能會不準，你要小心使用”。
問題二：為什么要關注不確定度建模？
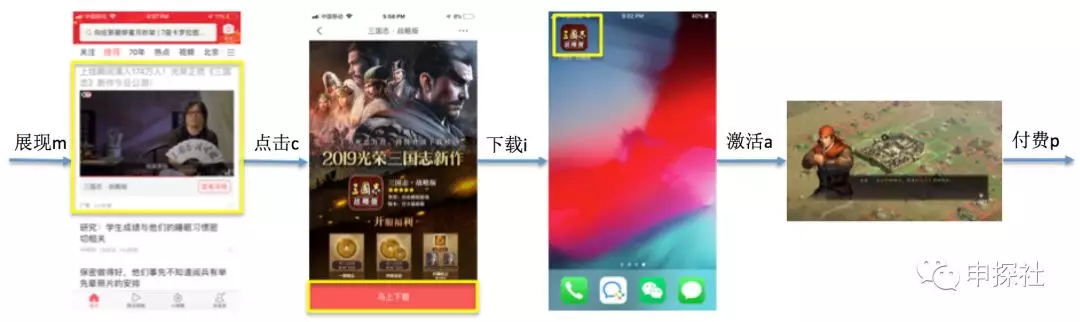
在廣告系統中，對于不確定度的建模，雖然沒有CXR建模來說那么關鍵，但是隨著兩個趨勢的發展，也越來越重要了。第一個趨勢是廣告主要優化的鏈路深度越來越深（以前優化到激活就可以，現在要優化到付費，付費金額），而后鏈路數據越往后越稀疏。廣告主的深度鏈路優化需求，就像-11034米的馬里亞納海溝，我們對它的觀測數據非常稀少，那里有什么東西的不確定度非常大。第二個趨勢是廣告素材逐漸從圖文載體向衰減速度更快的短視頻載體遷移。廣告主必須不斷上新素材，新素材占比越來越高。更深的后鏈路事件，會讓CvR的樣本更加稀疏；而新素材也就意味著素材的行為數據更加稀少，相關的CXR樣本更加稀疏 。這個時候，怎么能通過不確定度來區分對待置信和不置信的預估值，就變得更加重要了。
問題三：不確定度可以怎么用？
不確定度在廣告系統中的應用可以大概分為兩類：一是在探索與利用（E&E）中，用來更有效率地降低不確定度；二是基于不確定度進行策略決策。
我們先來看第一類應用，在此之前先介紹下不確定度建模的一個最簡單的方法：
其中n為包含目標對象（item）的樣本數。在實際工作里，很多時候用這個簡單的方法來估計不確定度就夠了。在很多經典算法里，實時上也是近似地用了這個公式，例如E&E里UCB算法。假設我們要估計剛才那兩個廣告點擊率的不確定度，n就等于每個廣告的曝光次數，那么廣告A的不確定度為?
?，而廣告B的不確定度只有
，是廣告A的十分之一。廣告B比廣告A曝光增加了100倍，不確定度只變成原來1/10，而不是1/100。所以我們可以發現，隨著曝光的增加，不確定的下降速度是慢慢降低的。而最開始的幾次曝光，讓不確定度下降得最明顯。如果我們的目標是讓所有廣告總的不確定度下降最多的話，那么選已曝光次數少的（也就是不確定度高的，帶來信息量大的），是效率比較高的方式。所以很多E&E策略，在探索的時候會根據item不確定度值的高低，來決定item被探索的概率。當然，不確定度只是決定探索概率的一個重要因素，還有很多其他因素也需要考慮，但不是本文重點，不再贅述。
可是這種最簡單的不確定建模方式的問題是，完全忽略了item之間的關系。例如廣告A和廣告B很相似，我們推一下極端，假設它兩完全一樣：都用了素材A，都推廣產品B，定向出價都是一樣的。那么如果廣告A已經被展現了300次，有100次點擊，點擊率是1/3。理想情況下，即使廣告B完全沒有展現，它的點擊率預估值的不確定度也應該是和廣告A一樣的（廣告B借用了廣告A的展現數據來降低了自己預估值的不確定度）。但是用上面簡單的方法，不確定度還是（其中n=0），也就是無窮大。如果廣告B只是和廣告A用一樣的素材，但定向出價是不一樣的。那么廣告B預估值的不確定度應該是大于廣告A的不確定度，但是小于無窮大。所以為了得到更加精細的不確定度，就得考慮有泛化能力的不確定度建模方法，可以把其他相似廣告的不確定度泛化到目標廣告。這些更復雜的建模方法和的差異大不大呢？基本上可以認為跟用點擊率預估模型來預估一個廣告的點擊率和用這個廣告自己的后驗數據（點擊數/展現數）來預估這個廣告點擊率的差異差不多。值不值得做，就看具體業務場景的需求了。
如果使用了有泛化能力的不確定建模方法，除了得到一個更準確的不確定度預估值之外，還有一個好處是，我們在選擇探索的item的時候，可以主動選擇那些可以將不確定度泛化給更多其他item的item來進行探索（例如與很多其他item都相似的item），探索完一個item，可以降低一批item的不確定度，從而提高每次探索能降低的總不確定度。就像農藥里蔡文姬的二技能“彈彈彈”，攻擊一個敵人，傷害一群敵人。
在廣告系統中，除了廣告冷啟動，還有很多需要做E&E的地方，都可能會用到不確定度，例如其他緯度冷啟動（如素材冷啟動，用戶冷啟動），投放系統E&E，模型訓練/投放系統的超參數搜索，智能擴量等等。另外，不確定度建模在強化學習里，也有成熟的應用。例如強化學習里agent在一個environment學習，為了提高學習效率，需要盡量走到不確定性高的地方（類似E&E場景），這樣能收集到的樣本帶來的信息量最大。
接下來，我們看看不確定度的第二類應用場景，基于不確定度進行策略決策。
為什么在決策中只考慮預估值不夠，也需要考慮不確定度呢？舉個例子來說，坐公交車到公司平均需要30分鐘，但是可能因為堵車需要40分鐘，也可能因為一路綠燈，只需要20分鐘。坐地鐵也平均需要30分鐘，但是幾乎不受其他因素影響，非常準時。顯而易見，坐公交車上班為30分鐘的不確定度要大于坐地鐵上班為30分鐘的不確定度。如果要上班不遲到，坐公交車就得提早40分鐘出門，而坐地鐵只需要提早30分鐘。這就是決策不能只考慮期望值，也得考慮不確定度的一個例子。
對于廣告來說，以剛才的例子來說，廣告B的點擊率為1/3已經很確定了，如果成本是達標的，那么投放系統就可以大膽放量了。對于廣告A的點擊率為1/3，是還不太確定的，可能更高，可能更低。為了不要超成本，廣告系統的一個可能更優的選擇是通過出比廣告B稍微低一些的價格保守投放廣告A，等到積累的展現點擊數更多了，再大膽投放。在廣告系統中，智能出價，智能定向等等產品中都可能會用到不確定度進行策略決策。
本文最終要介紹的貝葉斯神經網絡（BNN）是一種用神經網絡（當然也可以不用神經網絡，只是那樣文章估計沒人要看）來建模不確定度的模型，這個模型的輸入和普通模型一樣，但是輸出的是一個預估值的分布而不是單獨的一個預估值。有了這個預估值的分布，我們也可以再算出分布的期望值作為最終預估值，也可以得到這個分布的方差來表征的不確定度。預估出來的是分布，網絡中的權重也是分布（在具體實現的時候，權重和預估值的分布，大多數是通過從分布中采樣的樣本集來近似表示）。
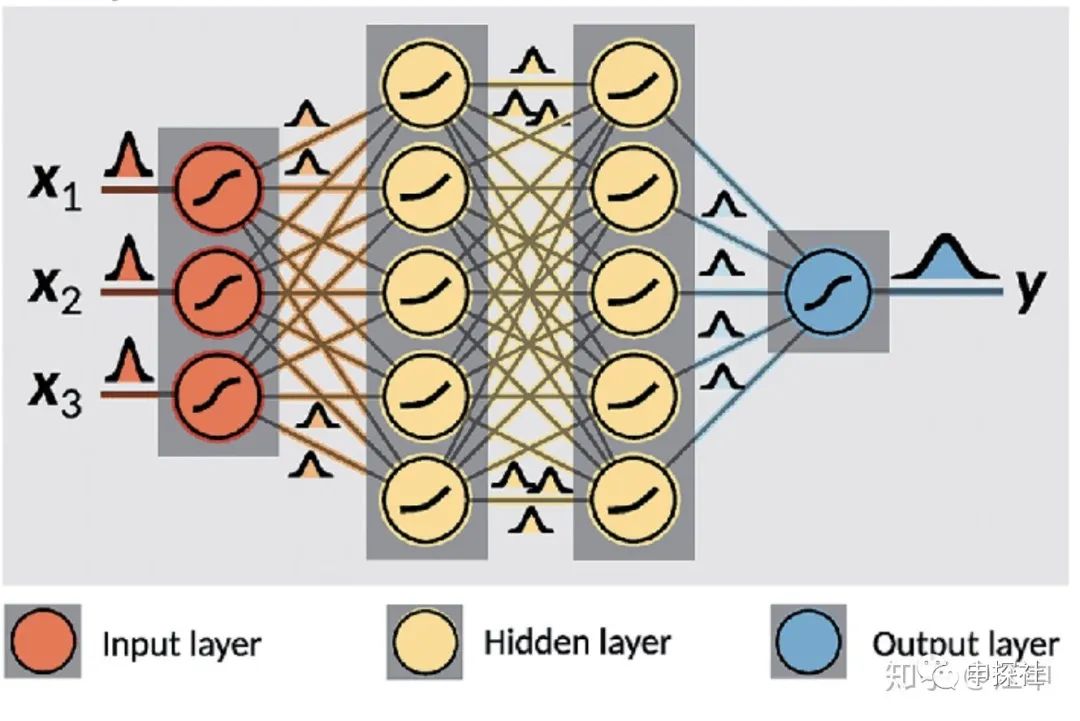
（圖片來源鏈接：https://www.researchgate.net/publication/329843608_How_machine_learning_can_assist_the_interpretation_of_ab_initio_molecular_dynamics_simulations_and_conceptual_understanding_of_chemistry）
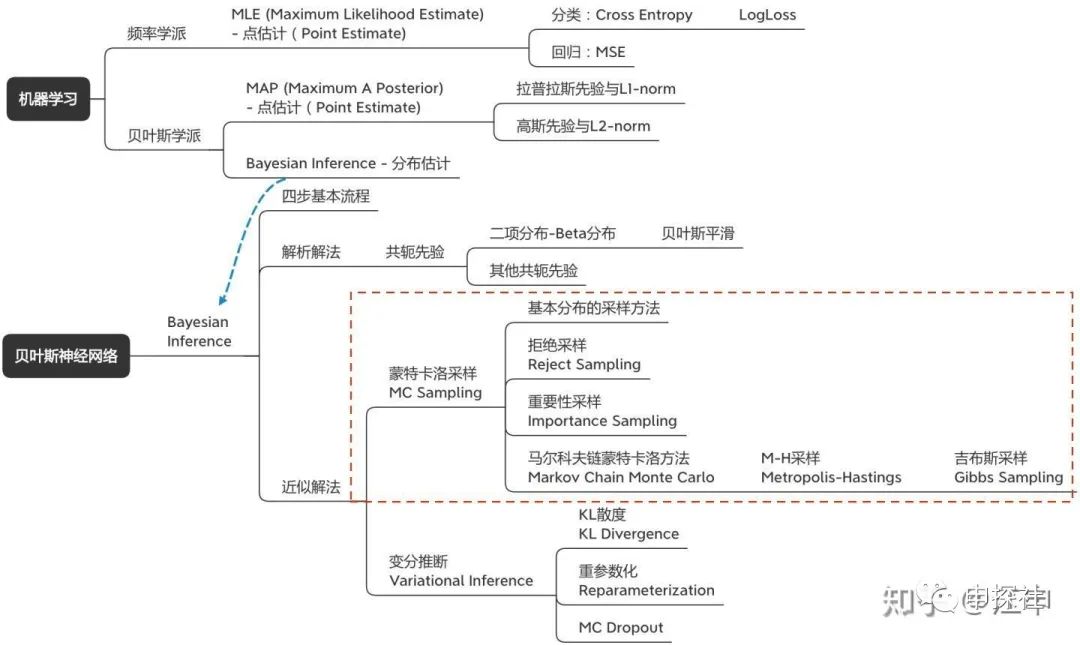
貝葉斯神經網絡涉及到的概念樹大概長下面這個樣子。里面有很多概念其實每一個單獨自身也是非常有意思的話題。我自己覺得這篇文章可能一方面是希望把貝葉斯神經網絡講明白，而逐漸把涉及的概念講清楚；從另外一個角度來說，也是想把這些有意思的概念通過一個結構給串起來（喬布斯的connecting the dots)。因為只有成結構的知識體系，才比較容易被理解和記憶。為了保證大家理解的順暢度，本文盡量保證全文用統一的一套數學標記和符號，因此公式全部重新手打，難免有錯誤的地方，歡迎大家指出。
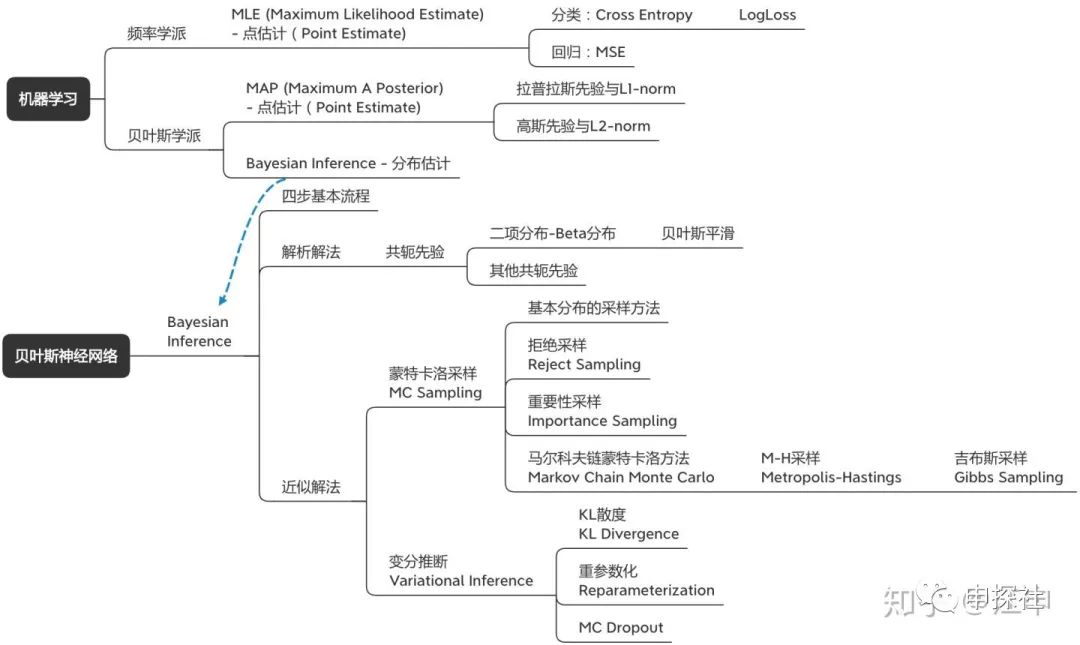
廢話不多說，我們的旅程從經典的貝葉斯公式開始：
（對于沒有見過這個公式的朋友，可能本系列的文章讀起來會有些吃力了。）
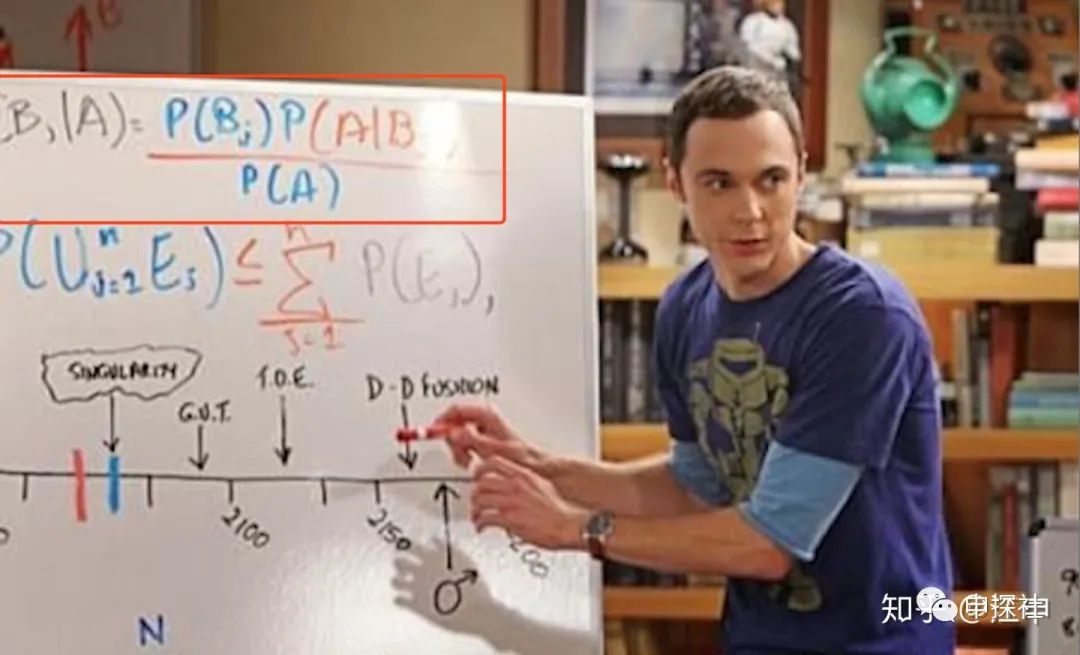
這個公式里，D是觀察數據或者是訓練的樣本，?
?是模型的參數。?
?叫似然率（Likelihood)，?
?叫先驗(Prior)，?
?叫后驗(Posterior)，?
?叫證據（Evidence)。
很多的資料上有所謂頻率學派與貝葉斯學派之分，但其實現在很少有人會區分這兩者。通常來說，頻率學派從最大似然率的角度來訓練模型(MLE)，而貝葉斯學派通常用兩種方法，一種是最大后驗概率(MAP)，另外一種是貝葉斯推斷（Bayesian Inference)。
一. 最大似然估計（MLE）
大家平時經常使用的幾種Loss，例如交叉熵，LogLoss，MSE（Mean Square Error）其實都是某種分布假設下的MLE。也就是說，大多數時候，大家通常是站在頻率學派的角度。接下來我們通過公式推導來展現他們之間的關系。對推公式不感興趣的讀者，也可以跳過證明的部分，記得黑體字的結論就可以了。
1. 最小化交叉熵=最小化KL散度=最大似然估計（MLE）
其中?
?(簡寫為P)就是真實值的分布，?
?(簡寫為Q)是預估模型預估值的分布，?
?就是P分布和Q分布的交叉熵。如下面的公式，根據交叉熵的定義，可以把H(P,Q)展開為P的熵H(P)和P到Q的KL散度?
?之和。因為H(P)即真實分布的熵與??無關（?
?是個常數），因此最小化他們的交叉熵，就等于最小化P到Q的KL散度。
我們把P和Q的簡寫展開，再把KL的定義帶入，則有
這里需要回顧一下微積分公式?
?，當x的分布是p(x)時，這個積分求出來的就是f(x)的均值。所以有
我們的訓練樣本?
?就是從真實樣本中采樣得到的，因此有
同樣的，?
?與??無關，所以可以從argmin里去掉，則有
上式就是最大似然估計，得證！
2. Log Loss是在二分類情況下的交叉熵（Cross Entropy)
對于比如點擊率預估來說，P和Q都服從伯努利分布。也就是說
?，
則
上式也叫做Log Loss，即Log Loss是在二分類情況下的交叉熵（Cross Entropy)。因此最小化Log Loss本質上也是最大似然估計（MLE）
3. 如果我們用正態分布來建模預估值，
?，其中?
那么似然率就是：
最大化上式（即MLE），等于最小化?
?，即MSE。
通過上面三個證明，把大家平時用得最多的交叉熵，logloss， MSE作為loss的方法，都歸到了MLE的范圍內。MLE最大的特點就是不考慮先驗分布。接下來我們看看把先驗分布納入會發生什么變化。
二. 最大后驗概率（MAP）
接下來我們來討論最大后驗概率MAP（Maximize a Posterior), 所謂后驗（Posterior) 即下面這個式子
因為?
?是與參數??無關的量，因此求argmax的時候可以把P(D)去掉，即：
我們可以看到MAP和MLE的區別，就在于后面乘了一個先驗?
?。這個先驗的作用是在訓練數據不充分的時候，讓參數有一個更加符合先驗假設的值，防止參數過擬合。說到防止過擬合，大家可能都會想到最經典的L1-norm和L2-norm。事實上，我們可以證明，如果先驗選擇協方差矩陣為單位矩陣常數倍的高斯分布，則MAP=MLE+L2-norm，而如果先驗選擇協方差矩陣為單位矩陣常數倍的拉普拉斯分布，則MAP=MLE+L1-norm。
證明如下：
因為?為協方差矩陣為單位矩陣常數倍的高斯分布，即
展開高斯分布則有
其中?
替代了那一堆常數，??也就是L2-norm正則項前面的系數。得證！
同理，如果先驗??選擇拉普拉斯分布，則有
同樣地，展開拉普拉斯分布
其中?替代了那一堆常數，??也就是L1-norm正則項前面的系數。得證！
MAP相比MLE，用先驗起到了類似正則項的作用，控制模型不過擬合。MAP的全稱是maximium a posteriori, 這里的A表示這只是最大化了其中一個點，有時候這會引發一些問題。舉個例子，假設后驗分布隨著參數??的變化的分布如下圖：
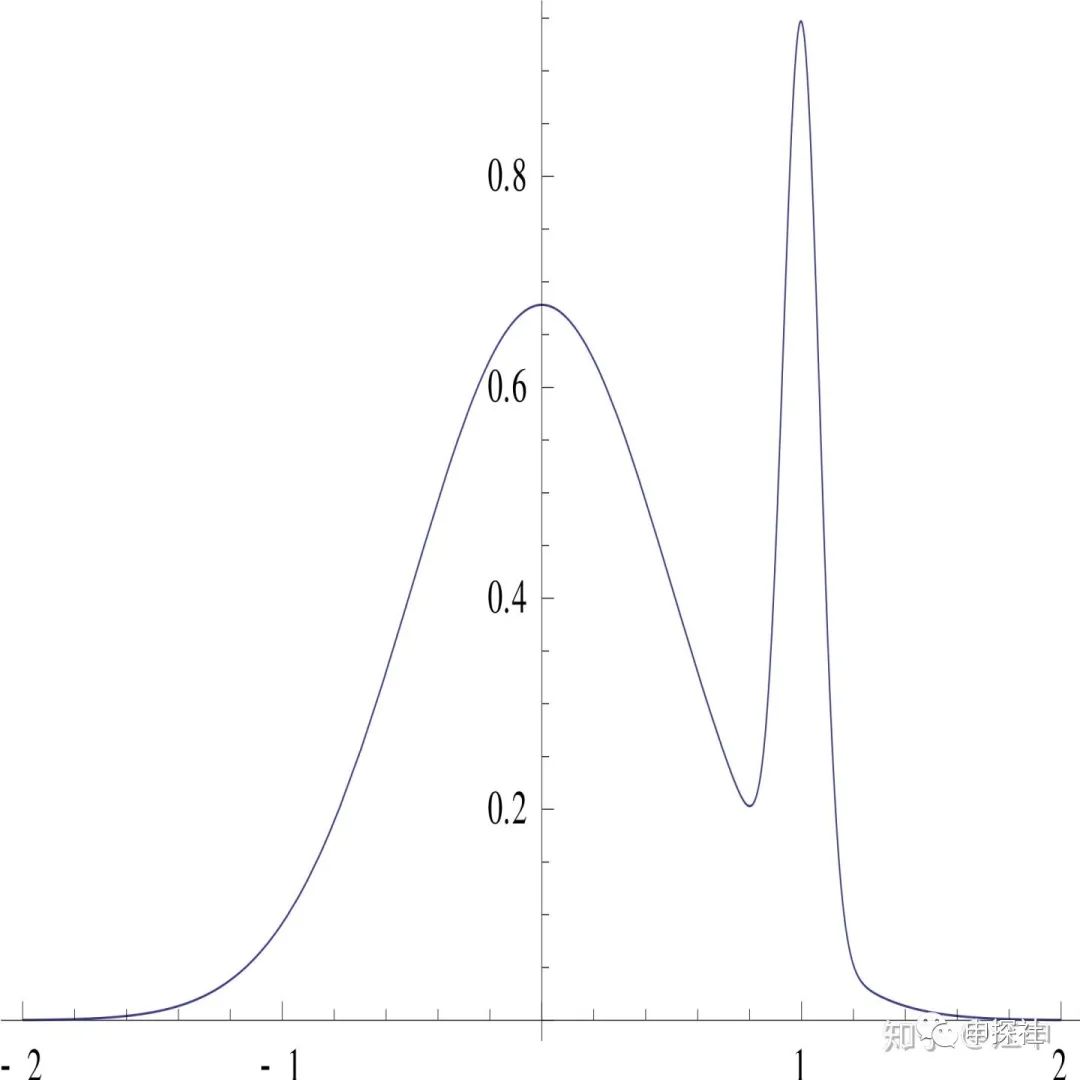
那么如果用MAP選出來的?就會是1，而我們通過觀察上圖，會發現0其實才是更好的選擇。大部分的概率密度是分布在0附近，1其實更像是個異常點。這就是點估計帶來的局限性，沒有考慮整個分布的形狀，只用了1個數來取代了整個分布。如果要考慮整個分布，那么不能只學習一個??, 而是要把??的整個分布學習下來，再用整個的分布去做預估。所以更加理論完美的方式是用貝葉斯推斷。
三、貝葉斯推斷
貝葉斯推斷通常遵循以下的四步：
第一步：假設先驗?
第二步：計算后驗?
展開后有?
第三步：計算預測值的分布?
第四步：計算y的期望值??；
如果需要，計算y的方差??作為預估值的不確定度
為了對比，我們把MAP的也列一下：
第一步：假設先驗?
第二步：計算讓后驗?
第三步：將帶入
中。對于很多
對比后可以發現，點估計（MLE或者MAP）相比貝葉斯推斷，最主要的區別在于只用了一個點?
?來代替整個??的分布，這個分布是否分散（不確定度是否高）的信息就被丟掉了。而在貝葉斯推斷里，我們可以認為是按照這個分布采樣了無數個?
?，對每個都計算出對應的
，然后再把所有的平均起來，得到最終的，也會比點估計得到的更加的準確。（當然，代價就是計算復雜度要高很多）
如果每個是一個創造營的觀眾的話，的分布就是觀眾的分布。點估計就好比在所有觀眾里，找一個最有代表性的觀眾，用他對練習生的投票的分布，作為最終練習生的排名。而貝葉斯推斷里可以認為每個觀眾的投票分布是，我們把所有觀眾的投票匯總，得到最終的總排名分布，要比最有代表性觀眾的投票更能反映練習生的受歡迎程度。
四、貝葉斯平滑
接下來，我們舉個完整的例子，來對比下MLE，MAP和貝葉斯推斷。在廣告或者推薦里，我們經常需要根據歷史展現數n，點擊數k，來估計一個廣告或者item的點擊率（比如作為統計特征加到模型里）。我們把這個要估計的點擊率，作為點擊率預估模型的唯一參數，接下來我們分別用MLE，MAP，貝葉斯推斷來估計這個參數和使用這個參數來對點擊率進行預估。也會引出工作中經常用到的貝葉斯平滑方法（很多人可能不知道，它其實是完整應用了貝葉斯推斷推導出來的）
（1）MLE
首先，我們需要對似然率建模?建模，很自然的選擇是Bernoulli分布（Bernoulli分布是Binomial在n=1時候的特例），Bernoulli分布就是專門用來刻畫這類問題，它唯一的參數就是點擊率?。
下面我們用MLE來做參數估計（訓練得到??的值），當n>1時，Bernoulli分布就變成了Binomial分布，我們把它展開就是:
其中
?是常數，對于計算argmax來說可以直接忽略。再用一下算法從業人員的老朋友: 取log操作。因為log是單調函數，取log不影響計算?
對上面這個式子取導數，令導數為0，就可以知道當
的時候，上面的式子可以取到最大值。
這個式子的意思就是，對于點擊率預估，如果用MLE的方法，就用點擊數除以展現數就好了。所以我們平時從直覺出發得到的結論，其實是有理論支撐的。不過如果點擊數是1，展現數是2，我們用MLE估計出來的點擊率就是0.5。一方面這個值很可能是偏高的（這個偏高是因為憑借我們對業務的理解，大概知道這個點擊率比如說是在0.1左右），另外一方面是這個0.5的預估的不確定度是比較高的（比較不準的）。解決第1個預估偏高的問題，我們可以通過MAP把先驗信息引入來解決。
（2）MAP
MAP和MLE的區別在于，最大化的不是似然率，而是似然率乘以先驗。在這里，我們先驗選擇的是Beta分布。似然率分布還是和MLE的一樣。
?，?
只所以做這樣的選擇，是因為Beta分布是Binomial分布的共軛先驗(Conjugate Prior)。什么叫共軛先驗呢？請看下面的公式（其中?
?函數叫Gamma函數，后面我們再介紹這個函數有什么性質）
我們把Binomial分布和Beta分布都展開，就會發現一開始Binomial分布是?
?的形態(a,b,c都與??無關），與Beta分布相乘之后，還是的形態（只是c, a, b的值不一樣了。只要滿足這個性質，我們就可以說Beta分布是Binomial分布的共軛先驗。共軛先驗的最大的好處就是：好計算。當我們把計算出來的后驗當成下一次迭代的先驗的時候，再乘以下一次迭代里的似然率，得到的還是的形態，可以一直迭代下去，計算非常的方便。所以很多時候，某些分布（或者模型結構）的選擇，不一定都是因為這個分布或結構貼合當前的問題，有的時候純粹就是為了好計算。其他常見共軛分布可以見（wiki鏈接：https://en.wikipedia.org/wiki/Conjugate_prior）。
類似MLE里的計算，我們依次對argmin的式子進行忽略前面的常數，取log，再求導數，令導數為0。就可以求解出
這里的?
?和?
?是先驗分布的參數，從直覺上，我們也可以理解為?
?是虛擬的正樣本數，?
?虛擬的負樣本數。例如如果?和?分別選擇為11和91，那么如果在一個展現和點擊也沒有的時候，上式等于?
?，也就是說先驗知識告訴我們，如何沒有任何數據，那么點擊率的先驗在0.1左右。當n和k的數字逐漸增大，??和??的值影響就會越來越小，逐漸收斂到?
?。
（3）貝葉斯推斷（Bayesian Inference)
最后是貝葉斯推斷。先驗分布，似然率分布還是和上面MAP的保持一致。
?，?
和MAP不一樣的是，我們不是求讓后驗最大的??值，而是直接計算后驗分布。回顧一下后驗的公式是這樣的。
MAP階段之所以不用擔心??的計算是因為我們是求?
?，?和??無關所以可以不用管。但是現在要求完整的后驗分布，就不能不管了。我們把似然率和先驗分別展開，然后把和??無關的因素都提出來到前面，就有了下面的式子。
也不知道是巧合還是Beta分布設計的時候故意的，居然這個積分有下面的性質
第一類歐拉積分?
于是我們的??就可以簡化成下式
接下來，我們就可以計算后驗??，并把上面的式子代入，并約掉幾個分子和分母都出現的子項，就有
到這里后驗分布?就算出來了，可以看到后驗還是形如?。這就是共軛先驗帶來的好處。
第三步是計算預測值的分布，因為我們觀測到D后的預測值分布?
?是參數為?的Bernoulli 分布，因此預測值y的分布就是??的分布。好吧，嚴謹點證明如下：因為y只有0和1兩個取值，因此根據離散分布的期望值計算公式
到這里其實已經得到了想要的預測值的分布。
第四步就可以計算預測值的均值（或者方差了，方差就可以表示不確定度，但做貝葉斯平滑通常我們只使用均值）
翻開大一微積分課本，找到均值計算公式如下
又碰到了剛遇見的朋友：第一類歐拉積分，代入后有
這個時候還需要介紹??函數的一個性質，?
?，則有
經過這么一堆復雜的積分計算，結果居然如此優雅，這就是數學的魅力吧（需要設計一個如此精巧的beta函數）。就像不管內心多么復雜的女神奧黛麗赫本，永遠都是那么優雅從容。
和MAP類似，我們也可以理解為??是虛擬的正樣本數，??是虛擬的負樣本數。上面這個式子，也叫貝葉斯平滑，大家很可能已經在工作里用過，但是可能不知道它其實是完整應用了貝葉斯推斷推導出來的。
假設?和?分別選擇為10和90，那么如果在一個展現和點擊也沒有的時候，上式等于?
?。也就是說先驗知識告訴我們，如何沒有任何數據，那么點擊率的先驗在0.1左右。如果有20個點擊（k=20)，100個展現（n=100)，則點擊率為?
?。我們可以看到經過貝葉斯平滑后的點擊率是介于先驗點擊率0.1和似然點擊率0.2（20/100）之間。當n和k的數字逐漸增大，??和??的值影響就會越來越小，逐漸收斂到??。
我們可以發現，這里的??控制平滑結果是更相信先驗還是更相信似然點擊率：??越大，表示越相信先驗，也表示需要更多的觀察數據（展現和點擊數）才能讓結果偏離先驗；而?
?則控制了先驗的率是多少。
總結一下，用這三種方法去做??的參數估計（也等于率的預估值），結果為
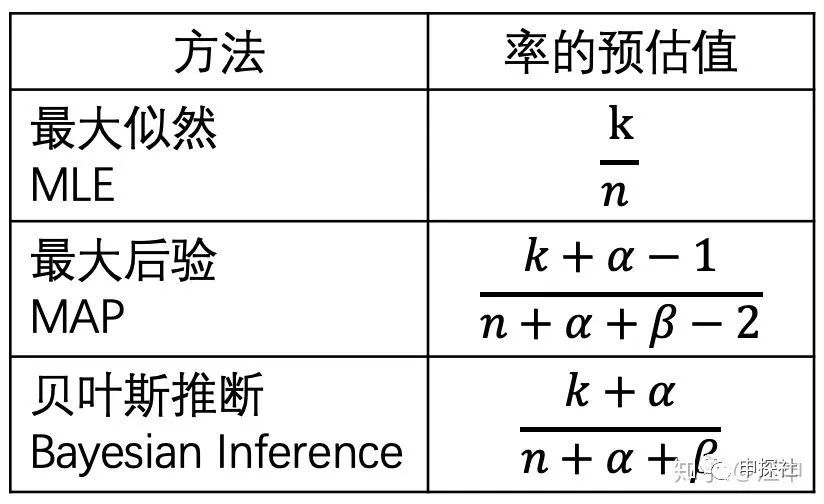
在推薦和廣告系統里，貝葉斯平滑可能是對各種CXR的統計類特征進行平滑最實用的方式。如果你還沒有用過，那么趕緊加入到你的工程師隨身攜帶工具箱吧。
對于?，?這兩個分布參數的選擇，不是本文的重點，因此本文只介紹一個最簡單其實也足夠實用的方法：矩估計。查詢下beta分布的wiki頁面（鏈接：https://en.wikipedia.org/wiki/Beta_distribution），會找到它的均值和方差分別是：
均值：
方差：?
然后我們直接對我們擁有的樣本，統計樣本均值（計為Mean）和樣本方差（計為Var），然后令
?，?
?，
然后解這個關于?
?的方程組，就可以算出??的值了：
有朋友可能會問，用來估計樣本均值和方差的樣本哪里來？我們不是要用貝葉斯平滑來平滑點擊率，就說明我們沒有足夠多的展現和點擊啊。答案是用其他場景的統計樣本來估計，例如要平滑某個新廣告單元下的點擊率，可以用這個賬戶歷史所有廣告單元的樣本來估計參數；又例如要平滑某個用戶的點擊率，可以用所有用戶的樣本來估計參數。
講到這里，我們終于把貝葉斯推斷講完了。不過通常貝葉斯推斷不能像貝葉斯平滑這樣優雅地直接推導出后驗分布，因為如果我們不是選擇了比較簡單的Bernoulli分布來建模和選擇Beta共軛先驗，剛好利用了這兩個分布的特性（第一類歐拉積分），那么在第三和第四步的兩個積分計算會很難求。因此我們需要借助一些近似算法來解決更加通用的情況，例如（中）（下）篇要討論的蒙特卡洛采樣法和變分推斷的方法。（下）篇中也會對實際應用中的一些問題進行討論。
（最后，友情提示：不要像文章封面圖片中的女孩那樣坐在懸崖邊的欄桿上，增加了太多的不確定度）
還是廣告
又到了招聘旺季，我們正在大力尋找志同道合的朋友一起在某手商業化做最有趣最前沿的廣告算法，初中高級廣告算法職位均有HC（迅速上車，還能趕上上市）
作者個人微信（添加注明申探社讀者及簡單介紹）：
歡迎掃描下面二維碼關注本公眾號，也歡迎關注知乎“申探社”專欄
文章為作者獨立觀點，不代表DLZ123立場。如有侵權,請聯系我們。( 版權為作者所有，如需轉載，請聯系作者 )
網站運營至今，離不開小伙伴們的支持。 為了給小伙伴們提供一個互相交流的平臺和資源的對接，特地開通了獨立站交流群。
群里有不少運營大神，不時會分享一些運營技巧，更有一些資源收藏愛好者不時分享一些優質的學習資料。
現在可以掃碼進群，備注【加群】。 ( 群完全免費，不廣告不賣課！)
