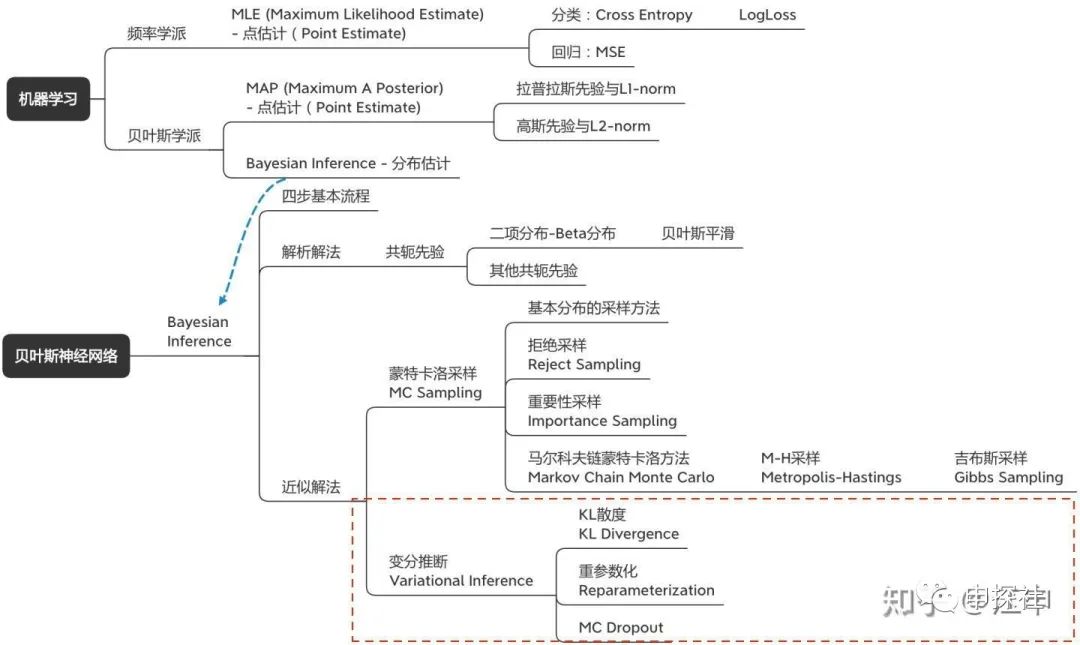
在(上)篇中,我們討論了什么是不確定度,為什么需要關(guān)注不確定度建模,以及不確定度可以怎么用。也從最大似然估計(jì)(MLE)到最大后驗(yàn)概率(MAP),講到了貝葉斯推斷(Bayesian Inference)。而我們希望用來(lái)建模不確定度的目標(biāo)模型是貝葉斯神經(jīng)網(wǎng)絡(luò)(BNN),它是一種用神經(jīng)網(wǎng)絡(luò)來(lái)建模似然率,然后進(jìn)行貝葉斯推斷的方法。(中)篇介紹了如何用蒙特卡洛采樣的方法來(lái)進(jìn)行貝葉斯推斷。而本篇會(huì)介紹另外一種方法:變分推斷。此外會(huì)講解一個(gè)非常容易實(shí)現(xiàn)的變分推斷特例:MC Dropout。也會(huì)討論在實(shí)際應(yīng)用貝葉斯神經(jīng)網(wǎng)絡(luò)(BNN)中的一些問(wèn)題。本篇涉及內(nèi)容主要是概念圖中的這一部分:
一. 變分推斷基本思想
回顧一下,在貝葉斯推斷中,我們主要的一個(gè)目標(biāo)是要計(jì)算后驗(yàn)概率










明星模仿者,通過(guò)不斷修正自己的發(fā)型,臉型,口音等等參數(shù),使得自己和明星的差距越來(lái)越小,最終就可以作為明星的“近似解”去上綜藝,做節(jié)目了。

這樣,我們的目標(biāo)就變?yōu)檎业阶?img data-ratio="0.425531914893617" src="https://cdn.dlz123.cn/uploads/images/2021-07-14/mmbiz_svg/LHdtlaBo22dZZjKKo6ia6GmmTPPk3tLE2JDsdsDY1fyicwsTt7oDoY6uUFpnyoszXRbsicGceAJ5KvUAIur8r6qaCyjtiaiczg2dj.svg" data-type="svg" data-w="47" style="vertical-align: middle;margin-right: 3px;margin-left: 3px;display: inline-block;">盡可能的接近




根據(jù)貝葉斯公式
帶入上式可以得到
根據(jù)期望值的計(jì)算公式?
如果我們引入一個(gè)專門的名稱ELBO,它等于(注意前面有個(gè)負(fù)號(hào))
則可以把優(yōu)化目標(biāo)寫成
因?yàn)?


所以我們的Loss就等于-ELBO就好了。不過(guò)ELBO里是三個(gè)期望值,而?
其中?

Notes 1:我們可以變換下ELBO的表達(dá)式,方便我們看看這個(gè)表達(dá)式內(nèi)在的含義。
可以發(fā)現(xiàn)后面那一項(xiàng)其實(shí)就是對(duì)數(shù)似然率,越大越好。前面那一項(xiàng)則是q分布和先驗(yàn)分布的KL散度,希望q分布和先驗(yàn)分布越近越好。似然率+先驗(yàn)約束,我們的老朋友。
Notes 2: 回憶一下上面的公式
變換下等式,有
因?yàn)??,所以有
回憶一下,在貝葉斯公式里,p(D)這一項(xiàng)叫evidence,而ELBO是p(D)取值的下界。這也是為什么叫ELBO(Evidence Lower Bound)的原因,
二. 用變分推斷訓(xùn)練貝葉斯神經(jīng)網(wǎng)絡(luò)
有了可計(jì)算的Loss,我們的建模方法很明確了:我們需要建一個(gè)神經(jīng)網(wǎng)絡(luò),它的可學(xué)習(xí)參數(shù)是?







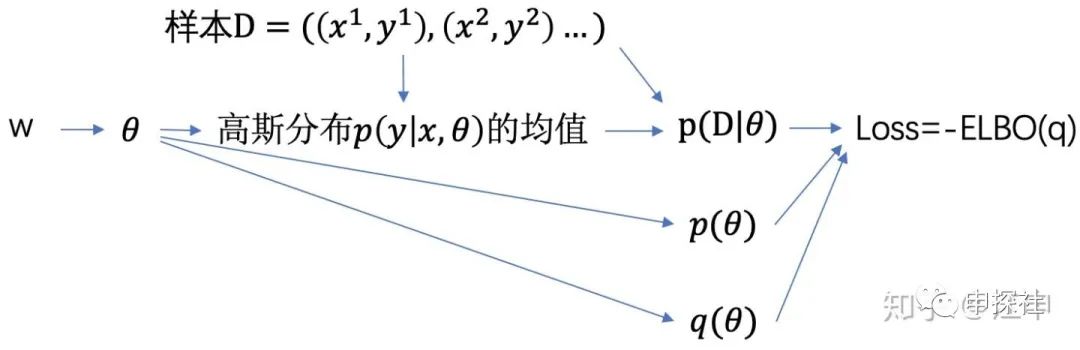
其中網(wǎng)絡(luò)中從?




那么?



我們把高斯分布做一個(gè)變換:?
這樣我們只需要從?




訓(xùn)練這個(gè)神經(jīng)網(wǎng)絡(luò),我們就可以得到最好的?




第一步:假設(shè)先驗(yàn)??,對(duì)似然率建模?
第二步:計(jì)算后驗(yàn)?
展開后有?
第三步:計(jì)算預(yù)測(cè)值的分布?
第四步:計(jì)算y的期望值??;
如果需要,計(jì)算y的方差??作為預(yù)估值的不確定度
我們完成了第二步,對(duì)于第三步和第四步,我們需要再次借助蒙特卡洛采樣的方法(不愧是二十世紀(jì)十大算法之一)。從

三. 變分推斷的代碼示例
(說(shuō)明:樣例代碼的原則是能說(shuō)明算法原理,追求可讀性,所以不會(huì)考慮可擴(kuò)展性,性能等因素。為了兼容用pytorch丹爐的朋友,訓(xùn)練方式用和pytorch更類似的接口。運(yùn)行環(huán)境為python 3,tf 2.3)
1. 構(gòu)造一些樣本,用來(lái)后面訓(xùn)練和展現(xiàn)效果。(此處參考了兩篇文章中的樣本產(chǎn)生和部分代碼,鏈接:krasserm.github.io/2019 及zhuanlan.zhihu.com/p/10)
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def f(x, sigma):
return 10 * np.sin(2 * np.pi * (x)) + np.random.randn(*x.shape) * sigma
num_of_samples = 64 # 樣本數(shù)
noise = 1.0 # 噪音規(guī)模
X = np.linspace(-0.5, 0.5, num_of_samples).reshape(-1, 1)
y_label = f(X, sigma=noise) # 樣本的label
y_truth = f(X, sigma=0.0) # 樣本的真實(shí)值
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X, y_truth, label='Ground Truth')
plt.title('Noisy training data and ground truth')
plt.legend();
2. 畫出的圖中,實(shí)線是y值的真實(shí)分布,“+”號(hào)是加上一定噪音后,我們觀測(cè)得到的樣本,也是后面訓(xùn)練用的樣本。

3. 與(中)篇的蒙特卡洛法一樣,先驗(yàn)分布選擇了一個(gè)由兩個(gè)高斯分布組成的混合高斯分布
不出意外?

其中?
這里對(duì)高斯分布的方差做了一些小設(shè)計(jì),據(jù)說(shuō)可以幫助?
from tensorflow.keras.activations import relu
from tensorflow.keras.optimizers import Adam
import tensorflow as tf
class BNN_VI():
def __init__(self, prior_sigma_1=1.5, prior_sigma_2=0.1, prior_pi=0.5):
# 先驗(yàn)分布假設(shè)的各種參數(shù)
self.prior_sigma_1 = prior_sigma_1
self.prior_sigma_2 = prior_sigma_2
self.prior_pi_1 = prior_pi
self.prior_pi_2 = 1.0 - prior_pi
# (w0_mu,w0_rho)是用來(lái)采樣w0的高斯分布的參數(shù),其他類似
self.w0_mu, self.b0_mu, self.w0_rho, self.b0_rho = self.init_weights([1, 5])
self.w1_mu, self.b1_mu, self.w1_rho, self.b1_rho = self.init_weights([5, 10])
self.w2_mu, self.b2_mu, self.w2_rho, self.b2_rho = self.init_weights([10, 1])
# 把所有的mu和rho放在一起好管理,模型里可學(xué)習(xí)參數(shù)是mu和rho,不是w和b
self.mu_list = [self.w0_mu, self.b0_mu, self.w1_mu, self.b1_mu, self.w2_mu, self.b2_mu]
self.rho_list = [self.w0_rho, self.b0_rho, self.w1_rho, self.b1_rho, self.w2_rho, self.b2_rho]
self.trainables = self.mu_list + self.rho_list
self.optimizer = Adam(0.08)
def init_weights(self, shape):
# 初始化可學(xué)習(xí)參數(shù)mu和rho們
w_mu = tf.Variable(tf.random.truncated_normal(shape, mean=0., stddev=1.))
b_mu = tf.Variable(tf.random.truncated_normal(shape[1:], mean=0., stddev=1.))
w_rho = tf.Variable(tf.zeros(shape))
b_rho = tf.Variable(tf.zeros(shape[1:]))
return w_mu, b_mu, w_rho, b_rho
def sample_w_b(self):
# 根據(jù)mu和rho們,采樣得到w和b們
self.w0 = self.w0_mu + tf.math.softplus(self.w0_rho) * tf.random.normal(self.w0_mu.shape)
self.b0 = self.b0_mu + tf.math.softplus(self.b0_rho) * tf.random.normal(self.b0_mu.shape)
self.w1 = self.w1_mu + tf.math.softplus(self.w1_rho) * tf.random.normal(self.w1_mu.shape)
self.b1 = self.b1_mu + tf.math.softplus(self.b1_rho) * tf.random.normal(self.b1_mu.shape)
self.w2 = self.w2_mu + tf.math.softplus(self.w2_rho) * tf.random.normal(self.w2_mu.shape)
self.b2 = self.b2_mu + tf.math.softplus(self.b2_rho) * tf.random.normal(self.b2_mu.shape)
self.w_b_list = [self.w0, self.b0, self.w1, self.b1, self.w2, self.b2]
def forward(self, X):
self.sample_w_b()
# 簡(jiǎn)單的3層神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)
x = relu(tf.matmul(X, self.w0) + self.b0)
x = relu(tf.matmul(x, self.w1) + self.b1)
self.y_pred = tf.matmul(x, self.w2) + self.b2
return self.y_pred
def prior(self, w):
# 先驗(yàn)分布假設(shè)
return self.prior_pi_1 * self.gaussian_pdf(w, 0.0, self.prior_sigma_1) \
+ self.prior_pi_2 * self.gaussian_pdf(w, 0.0, self.prior_sigma_2)
def gaussian_pdf(self, x, mu, sigma):
return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)
def get_loss(self, y_label):
self.loss = []
for (w_or_b, mu, rho) in zip(self.w_b_list, self.mu_list, self.rho_list):
# 這里的q_theta_w和文章對(duì)應(yīng),其中的w指的是(mu,rho), 而w_or_b中的w就是權(quán)重中的w
q_theta_w = tf.math.log(self.gaussian_pdf(w_or_b, mu, tf.math.softplus(rho)) + 1E-30)
p_theta = tf.math.log(self.prior(w_or_b) + 1E-30)
# 公式中三項(xiàng)中的兩項(xiàng)
self.loss.append(tf.math.reduce_sum(q_theta_w - p_theta))
p_d_theta = tf.math.reduce_sum(tf.math.log(self.gaussian_pdf(y_label, self.y_pred, 1.0) + 1E-30))
# 公式中三項(xiàng)中的另外一項(xiàng)
self.loss.append(tf.math.reduce_sum(-p_d_theta))
return tf.reduce_sum(self.loss)
def train(self, X, y_label):
loss_list = []
for _ in range(2000):
with tf.GradientTape() as g:
self.forward(X)
loss = self.get_loss(y_label)
gradients = g.gradient(loss, self.trainables)
self.optimizer.apply_gradients(zip(gradients, self.trainables))
loss_list.append(loss.numpy())
return loss_list
def predict(self, X):
return [self.forward(X) for _ in range(300)]
X = X.astype('float32')
y_label = y_label.astype('float32')
model = BNN_VI()
loss_list = model.train(X,y_label)
plt.plot(np.log(loss_list))
plt.grid()
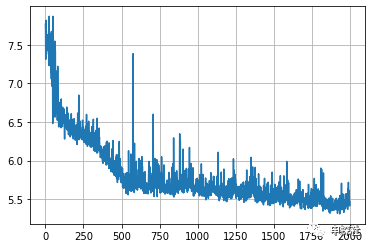
4. 畫出來(lái)的曲線是每一輪的loss
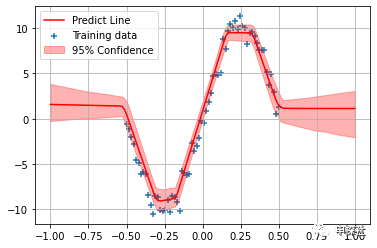
5. 預(yù)估階段,我們把預(yù)估的均值和不確定度都畫出來(lái)
X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_preds = model.predict(X_test)
y_preds = np.concatenate(y_preds, axis=1)
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()
6. 圖中,紅色線條就是所有BNN輸出值的均值,也就作為最終的預(yù)估值。而紅色的區(qū)域?qū)捳瑒t反應(yīng)了所有BNN輸出值的不確定度(為了方便可視化這里用分位數(shù))。可以看到,結(jié)果和(中)篇中蒙特卡洛采樣法得到的結(jié)果是類似的:對(duì)于沒(méi)有樣本的區(qū)域,不確定度較大,而對(duì)于樣本比較密集的地方,不確定度小。另外,在樣本有覆蓋的領(lǐng)域,轉(zhuǎn)彎的地方,因?yàn)橐x原來(lái)的路線,不確定度大;而直線的地方,則不確定度更小。
四. MC Dropout
前面介紹的蒙特卡洛采樣法和變分推斷的方法,實(shí)現(xiàn)起來(lái)都略顯復(fù)雜。對(duì)比之下,接下來(lái)介紹的這個(gè)方法,實(shí)現(xiàn)非常簡(jiǎn)單,適合工業(yè)界應(yīng)用。
這個(gè)方法的做法簡(jiǎn)單到只有兩句話:在原有的只預(yù)估均值的神經(jīng)網(wǎng)絡(luò)里,為每一層的所有權(quán)重都添加Dropout層,然后在預(yù)估(inference)的時(shí)候,讓dropout繼續(xù)生效。這樣同一個(gè)樣本,每次inference都會(huì)預(yù)估出不一樣的值(因?yàn)橛衐ropout),把這些值的均值,就作為預(yù)估值,這些值的方差,就作為預(yù)估值的不確定度。(Paper鏈接:proceedings.mlr.press/v)
這個(gè)做法,可以證明效果和變分推斷是等效的。不過(guò)盡管做法這么簡(jiǎn)單,但是這個(gè)證明卻非常復(fù)雜,感興趣的朋友可以看這個(gè)證明文檔(文檔鏈接:arxiv.org/pdf/1506.0215)
MC Dropout就像在巨無(wú)霸漢堡的每一層肉中間,都加上一層生菜。

我們介紹的訓(xùn)練貝葉斯神經(jīng)網(wǎng)絡(luò)的三種方法的異同如下

對(duì)于MC Dropout來(lái)說(shuō),也可以認(rèn)為在Inference階段,?

其中?
其中k為dropout的保留率。
因此MC Dropout作為一種變分推斷的一個(gè)特例,在這一點(diǎn)上是一致的,

五. MC Dropout代碼示例
1.(這里略去了生產(chǎn)樣本的代碼,和上面普通變分推斷的代碼是精確一致的)我們直接用keras的接口,像普通神經(jīng)網(wǎng)絡(luò)一樣把結(jié)構(gòu)搭建起來(lái),唯一的不同是每層之間都插入了Dropout層。
import tensorflow as tf
from tensorflow.keras.optimizers import Adam
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(1,1)),
tf.keras.layers.Dense(30, activation='tanh'),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Dense(30, activation='tanh'),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Dense(1, activation='linear')
])
model.compile(optimizer=Adam(learning_rate=0.1),
loss='mean_squared_error',
metrics=['MeanSquaredError'])
model.fit(X, y_label, epochs=2000)
2. 在預(yù)測(cè)的時(shí)候,通過(guò) training=True 這個(gè)設(shè)置,使得Dropout層在inference的時(shí)候,也會(huì)概率丟棄一部分節(jié)點(diǎn)。不設(shè)置這個(gè)參數(shù)的話,dropout層在inference的時(shí)候,默認(rèn)是會(huì)保留所有的節(jié)點(diǎn),不執(zhí)行dropout。
X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_preds = [model(X_test, training=True) for _ in range(300)]
y_preds = np.concatenate(y_preds, axis=1)
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()
3. 圖中,紅色線條就是所有BNN輸出值的均值,也就作為最終的預(yù)估值。而紅色的區(qū)域?qū)捳瑒t反應(yīng)了所有BNN輸出值的不確定度(為了方便可視化這里用分位數(shù))。可以看到,結(jié)果和(中)篇中蒙特卡洛采樣法或普通變分推斷的結(jié)果是一樣的。

六. 不確定度建模實(shí)際應(yīng)用中的一些問(wèn)題
(1) 對(duì)現(xiàn)有系統(tǒng)侵入性
不管是蒙特卡洛采樣法還是普通的變分推斷,對(duì)原有的CXR模型來(lái)說(shuō),都需要對(duì)模型結(jié)構(gòu)或者訓(xùn)練流程做較大的改動(dòng)。這也是阻攔不確定性建模落地的主要原因。而MC Dropout對(duì)原有模型的侵入型很小,比較方便落地。對(duì)于添加的dropout層,也許本來(lái)也可以幫助模型抑制過(guò)擬合,而提高預(yù)估的準(zhǔn)確性。
(2) 性能問(wèn)題
相比普通的模型,貝葉斯神經(jīng)網(wǎng)絡(luò)要預(yù)估出很多個(gè)值,再求方差來(lái)作為不確定度的度量,在線inference時(shí)的計(jì)算量會(huì)翻幾倍,對(duì)性能會(huì)有較大影響。可以考慮做以下幾點(diǎn)的優(yōu)化來(lái)緩解性能問(wèn)題:
1. 只在最頂上幾層添加dropout做tradeoff。雖然理論上不能保證和變分完全等效,但是在筆者的實(shí)驗(yàn)中,效果也是可接受的。
2. 原有模型不變,仍舊只預(yù)估期望值。單獨(dú)使用一個(gè)結(jié)構(gòu)更簡(jiǎn)單的模型,再加上dropout來(lái)預(yù)估不確定度。可以這么做是因?yàn)椴淮_定度的精度不需要那么高。另外這樣的好處是可以完全和原有模型結(jié)耦,0侵入性。但是缺點(diǎn)是這個(gè)更簡(jiǎn)單的模型,和原有模型不一致,不確定度和預(yù)估值不是一起訓(xùn)練出來(lái)的,可能會(huì)“不配套”。
3. 在線inference時(shí)每次inference是獨(dú)立的,可以進(jìn)行并行化。對(duì)于變分推斷(包括MC Dropout)可以先把?
4. 事實(shí)上,在很多實(shí)際應(yīng)用場(chǎng)景,因?yàn)閷?duì)不確定度的預(yù)估準(zhǔn)確度要求并不高,因此對(duì)實(shí)時(shí)性的要求也不高,我們可以通過(guò)離線計(jì)算來(lái)緩存不確定度,然后定期更新就好。例如我們主要關(guān)心新廣告的不確定度,則可以定期采樣一些涉及該廣告的請(qǐng)求,然后離線計(jì)算出這些請(qǐng)求的不確定度,再取平均(抹平人群和上下文差異)作為該廣告的不確定度。如果需要關(guān)心某人群與新廣告組合的不確定度,也可以如法炮制,離線統(tǒng)計(jì)人群與新廣告交叉緯度的平均不確定度。
(3)不確定度的預(yù)估準(zhǔn)確性評(píng)估
貝葉斯神經(jīng)網(wǎng)絡(luò)模型中用了不同的網(wǎng)絡(luò)結(jié)構(gòu),或者不同的超參數(shù),哪個(gè)模型預(yù)估的不確定度更準(zhǔn)確呢?要直接評(píng)估不確定度預(yù)估的準(zhǔn)確性不太容易,我們只好通過(guò)兩個(gè)間接評(píng)估的方法來(lái)評(píng)估。
直接評(píng)估不好評(píng)估,則考慮間接評(píng)估的例子如下。

方法一:如果我們是通過(guò)預(yù)估y值的分布,再用方差來(lái)作為不確定度的度量,則可以通過(guò)評(píng)估y值分布的準(zhǔn)確性來(lái)間接評(píng)估方差的準(zhǔn)確性。我們先用訓(xùn)練集進(jìn)行模型訓(xùn)練,然后在測(cè)試集上做評(píng)估。對(duì)有n個(gè)樣本的測(cè)試集中每個(gè)樣本?




如果我們的任務(wù)是regression,如前文所述,神經(jīng)網(wǎng)絡(luò)的輸出為高斯分布?

測(cè)試集的平均log似然率越高,說(shuō)明預(yù)估的y分布,和實(shí)際分布越符合。從直覺(jué)來(lái)看,當(dāng)對(duì)某個(gè)樣本的y值的預(yù)估方差較小時(shí),如果實(shí)際的y值方差較大,也就是落在離均值比較遠(yuǎn)的地方,則會(huì)有一個(gè)較低的似然率,從而懲罰偏小的預(yù)估方差;而當(dāng)預(yù)估方差較大時(shí),如果實(shí)際的y值方差較小,即y值都落在均值附近的地方,也會(huì)因?yàn)榫蹈浇怕拭芏缺环值粢徊糠值狡渌胤剑玫揭粋€(gè)較低的似然率,從而懲罰偏大的預(yù)估方差。
不過(guò)平均log似然率評(píng)估的是整個(gè)分布的預(yù)估準(zhǔn)確度,也包括了均值的預(yù)估準(zhǔn)確度。所以log似然率的提升,不一定是不確定度預(yù)估準(zhǔn)確性的提升。
方法二:直接評(píng)估不好評(píng)估,我們只好通過(guò)使用了不確定度預(yù)估值的任務(wù)的效果來(lái)間接評(píng)估了。下面用冷啟動(dòng)作為一個(gè)例子,但是其他的任務(wù)也都可以設(shè)計(jì)相應(yīng)的方法。在冷啟動(dòng)中,我們使用不確定度來(lái)決定探索哪些廣告,那么我們就可以根據(jù)探索的效率來(lái)評(píng)估不確定度預(yù)估的準(zhǔn)確度。
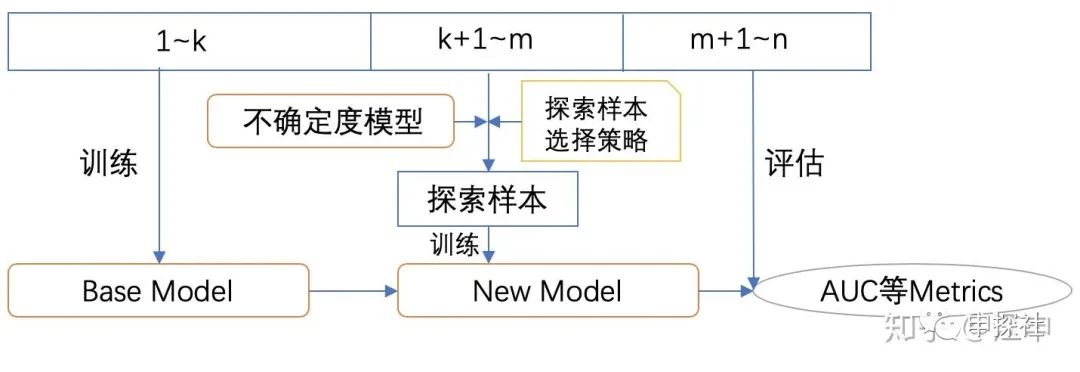
我們可以先用第1到第k天的樣本訓(xùn)練一個(gè)Base模型?









上面的這個(gè)流程的原理,是不是和Meta Learning的有些類似?如果我們把Base模型的模型結(jié)構(gòu)或超參數(shù),不確定度模型的結(jié)構(gòu)或者超參數(shù),以及探索樣本選擇策略,都作為meta模型的可學(xué)習(xí)參數(shù),我們就可以試圖去學(xué)一個(gè)好的學(xué)習(xí)方法,這個(gè)學(xué)習(xí)方法好不好,則可以通過(guò)在最終測(cè)試集上的AUC等metrics來(lái)評(píng)估。最終得到一個(gè)較好的學(xué)習(xí)方法,可以在同樣的探索成本下,獲得最高的模型效果提升,也就是冷啟動(dòng)探索效率的提升。
當(dāng)然,實(shí)際線上的冷啟動(dòng)任務(wù)比構(gòu)造的這個(gè)任務(wù)要更復(fù)雜,例如在這個(gè)任務(wù)中,通過(guò)限制探索樣本的數(shù)量來(lái)限制探索所需要的成本,而實(shí)際線上搜集每個(gè)樣本的成本是不相同的,數(shù)量一致不代表資源一致。
講到這里,本系列的主要內(nèi)容就介紹完了,感謝大家的支持。希望大家共同來(lái)探索不確定度建模在廣告系統(tǒng)中的應(yīng)用。
還是廣告
又到了招聘旺季,我們正在大力尋找志同道合的朋友一起在某手商業(yè)化做最有趣最前沿的廣告算法,初中高級(jí)廣告算法職位均有HC(迅速上車,還能趕上上市)。感興趣的朋友歡迎加我的個(gè)人微信約飯約咖啡索要JD或發(fā)送簡(jiǎn)歷。(產(chǎn)品和運(yùn)營(yíng)也在招人,看機(jī)會(huì)的朋友我可以幫忙直接推薦給leader們。)
作者個(gè)人微信(添加注明申探社讀者及簡(jiǎn)單介紹):

歡迎掃描下面二維碼關(guān)注本公眾號(hào),也歡迎關(guān)注知乎“申探社”專欄

文章為作者獨(dú)立觀點(diǎn),不代表DLZ123立場(chǎng)。如有侵權(quán),請(qǐng)聯(lián)系我們。( 版權(quán)為作者所有,如需轉(zhuǎn)載,請(qǐng)聯(lián)系作者 )

網(wǎng)站運(yùn)營(yíng)至今,離不開小伙伴們的支持。 為了給小伙伴們提供一個(gè)互相交流的平臺(tái)和資源的對(duì)接,特地開通了獨(dú)立站交流群。
群里有不少運(yùn)營(yíng)大神,不時(shí)會(huì)分享一些運(yùn)營(yíng)技巧,更有一些資源收藏愛(ài)好者不時(shí)分享一些優(yōu)質(zhì)的學(xué)習(xí)資料。
現(xiàn)在可以掃碼進(jìn)群,備注【加群】。 ( 群完全免費(fèi),不廣告不賣課!)